行星齿轮减速机是最常见的电机减速机。如图1所示，行星齿轮减速机包括太阳轮、行星轮、行星架和内齿圈四个主要部件构成。常见的工况下，力矩从太阳轮输入，内齿圈固定，行星轮轴固定在行星架上，太阳轮带动行星轮自转的同时，带动行星架围绕太阳轮公转，力矩从行星架输出。

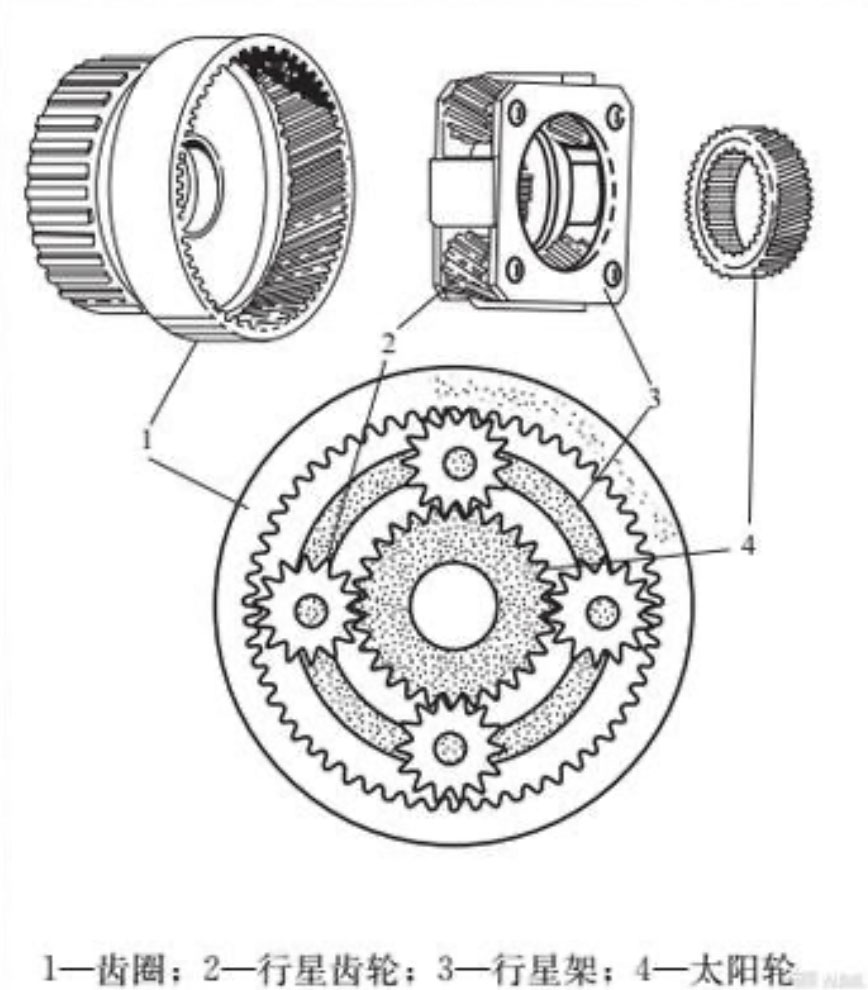
图1 行星齿轮减速机结构

一、行星齿轮的减速比推导

图2是一个行星减速机构的示意图。

r0为太阳轮半径，r1为行星轮半径，r2为内齿圈半径。

Zs为太阳轮齿数，Zr为齿圈齿数。

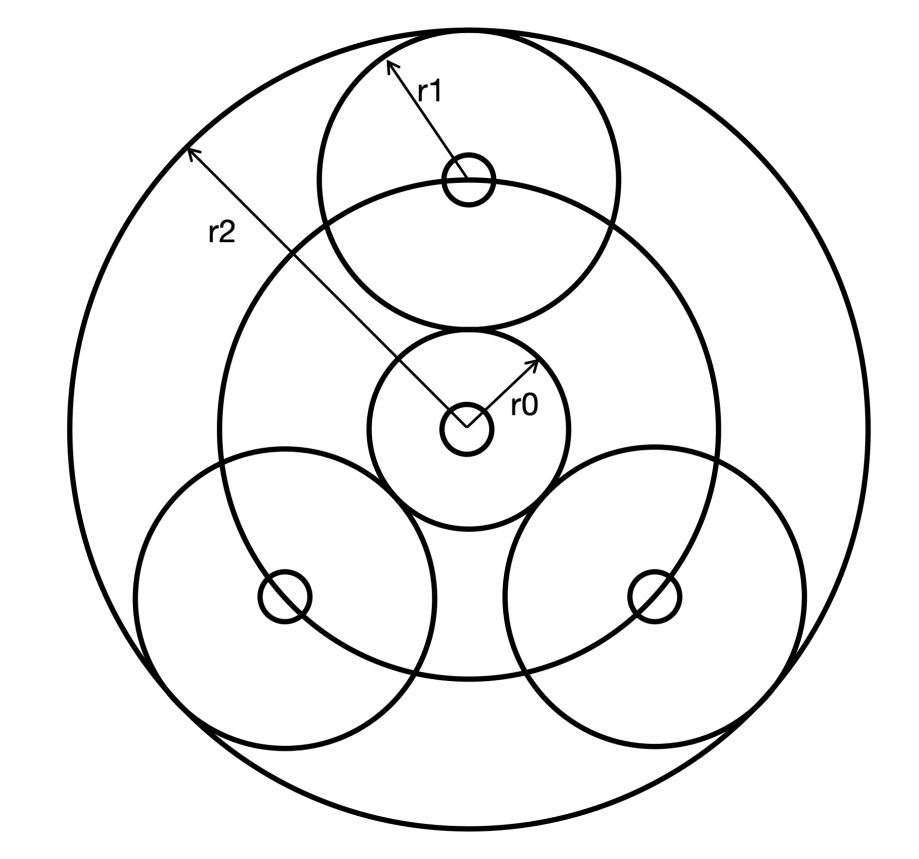
图2 行星减速机示意图

以下从两个角度来推导减速比。

（1）从齿轮啮合的行程来推导。

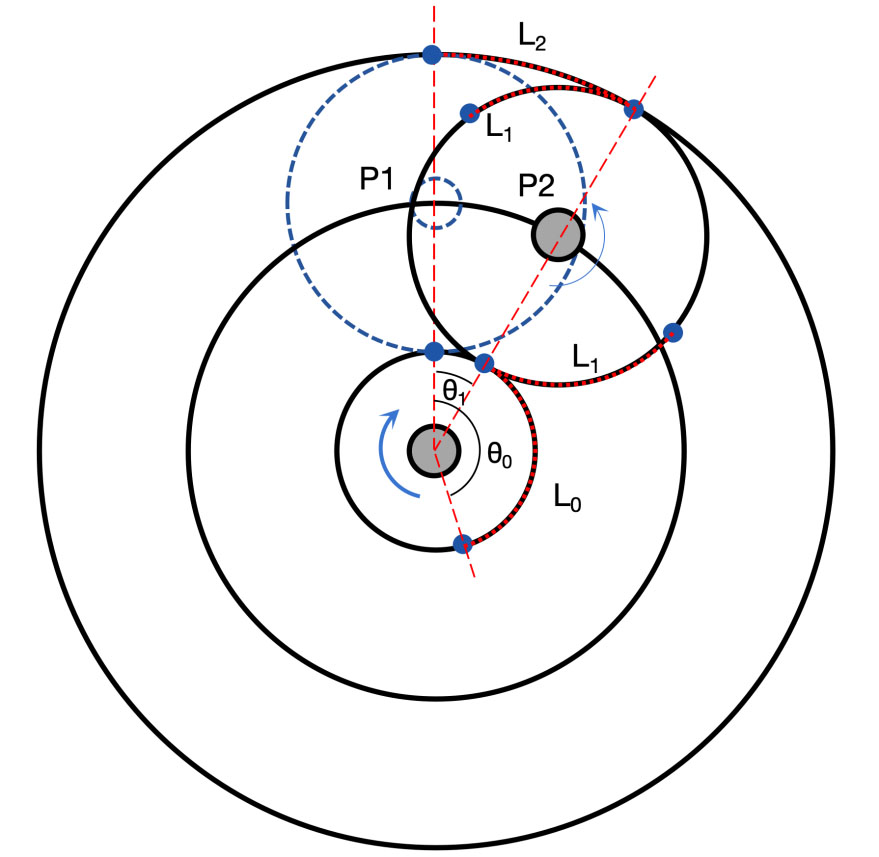
图3 行星减速机示意图

图3展示了太阳轮旋转θ0角度时，带动行星轮从P1位置移动到P2位置，行星架转动了θ1角度，其中，太阳轮和行星架顺时针旋转，行星轮逆时针旋转。在图3中，用红色的虚线圆弧标注了太阳轮、行星轮、内齿圈齿轮啮合的轨迹，长度分别是L0、L1和L2，显然有：

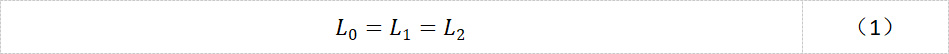
对太阳轮有：

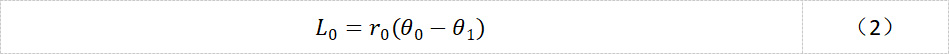
对内齿圈有：

因此减速比

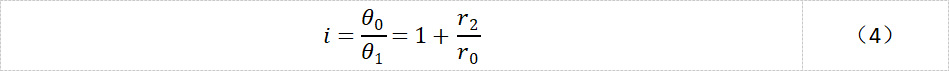
而由于齿轮相互啮合，所以齿数比等于半径比，即：

所以：

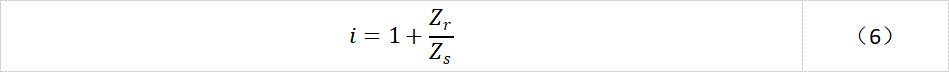
也就是说，行星齿轮的减速比等于内齿圈和太阳轮齿数比加1。

（2）从功率角度推导。

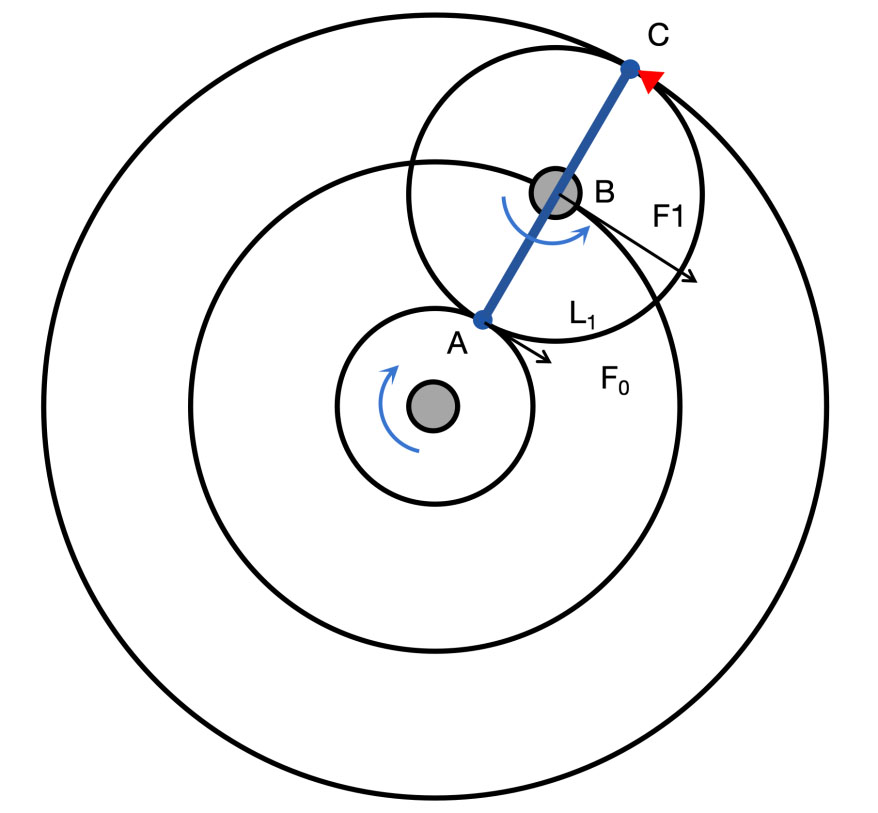
图4 行星减速机示意图

假设输入轴的功率为P0，输入转矩为T0，太阳轮转速为ω0。

那么在太阳轮和行星轮的接触点，行星轮受到的切向力为F0，n为行星轮的个数。

这时的行星轮可以看成一个杠杆ABC，支点在C点，在A点输入力F0，在B点输出力F1应为F0的两倍，那么：

行星轮对行星架施加的总力矩T1的做功功率为P1，行星架转速为ω1.那么：

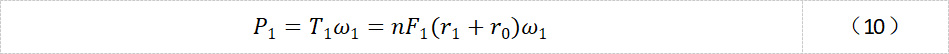
当系统不存在能量损耗时：

于是：

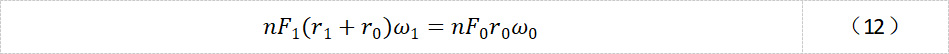
那么减速比：

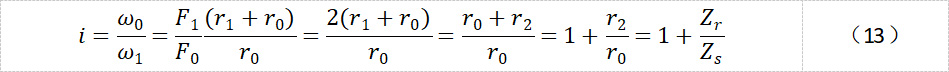
二、行星齿轮减速器的优势

（1）分散力矩，降低单个齿应力。可以看到对于平行轴减速机，输入/出齿的力矩全部施加在单个齿上，应力也集中在这个接触点上。但是对于行星减速机，同样的输入/出力矩分散在多个行星轮与太阳轮/内齿圈的接触齿上，降低了单个齿的应力。

如图5所示，两个单级减速机构的输入力矩相同，但行星减速机输入齿的局部应力是平行轴减速机的1/3倍，继续增加行星轮还能降得更低。对于输出齿也是同样的道理。

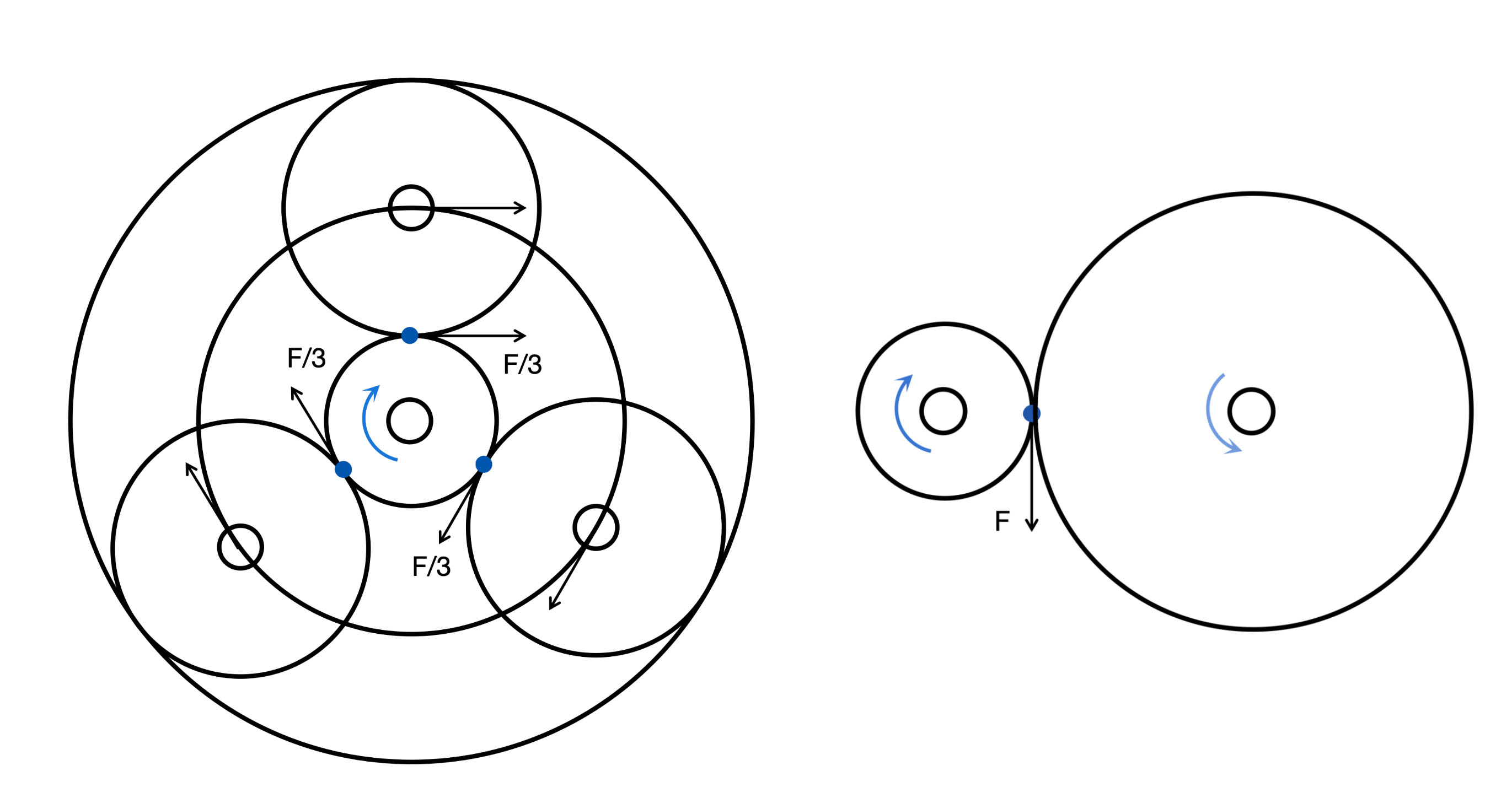
图5 行星减速机和平行轴减速机的输入/出齿受力示意图

（2）轴的径向合力为零，仅仅受到到扭矩，相同轴可以输出更大的扭矩。我们在画示意图时，两个齿轮之间的作用力都当做切向力来处理，但实际上，齿轮啮合过程中的合力并非切向，而是会在径向有个分力。如图6所示，平行轴减速机的输入齿受到一个径向的分力，这个力通过齿轮传递到轴承再传递到轴，对轴和轴承都会造成额外的负担，降低系统的寿命，所以设计时只能增加轴径进行补偿。而行星齿轮减速机的输入齿，虽然每个接触点都有径向分力，但这几个分力关于轴心对称，因而相互抵消，从而使得轴以及轴承在径向上没有受力，仅承担扭矩，因此轴和轴承都可以用更细的尺寸。对于输出轴也是一样的道理。

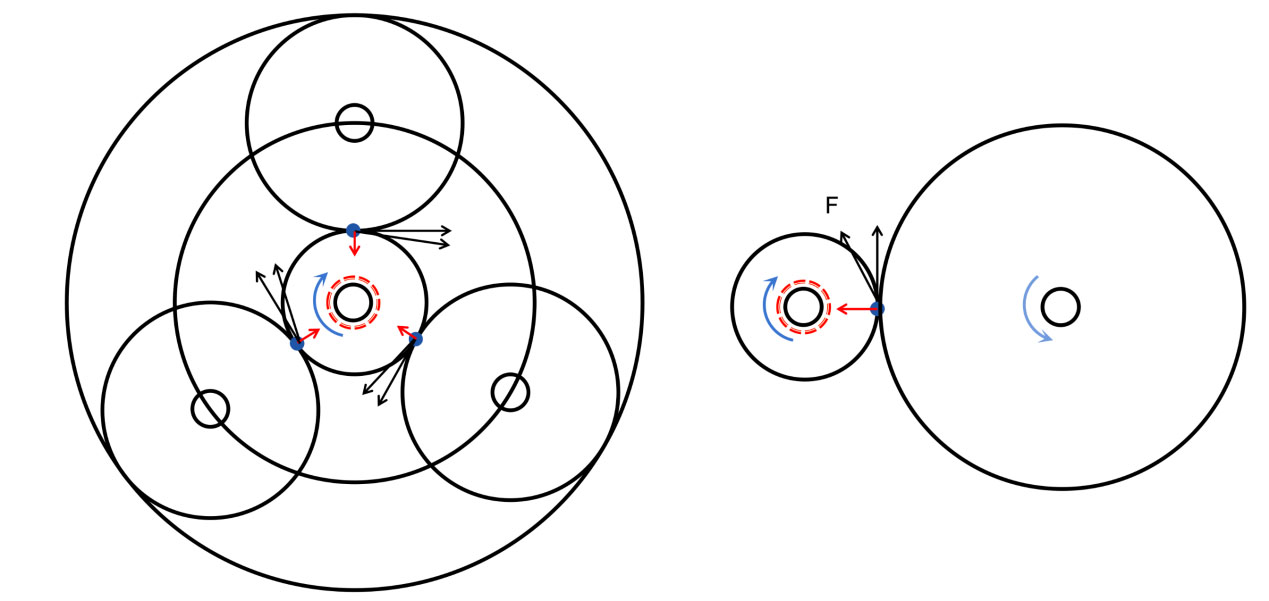
图6 行星减速机和平行轴减速机的输入齿的受力分解示意

结构紧凑，小尺寸实现大减速比。行星齿轮减速机的大齿轮和小齿轮同轴，不同级的减速机构可以叠放，因此结构非常紧凑。而对于普通平行轴减速机，齿轮轴不能和齿轮盘干涉，所以整体尺寸较大，空间利用率较低。如图7所示，对于单级减速比为i的减速机构而言，行星齿轮机构的尺寸为平行轴减速机构尺寸的(i-1)/(i+1)，以i=5为例，那么前者是后者尺寸的2/3，尺寸降低33%。随着减速级数增加，尺寸减幅将进一步扩大。

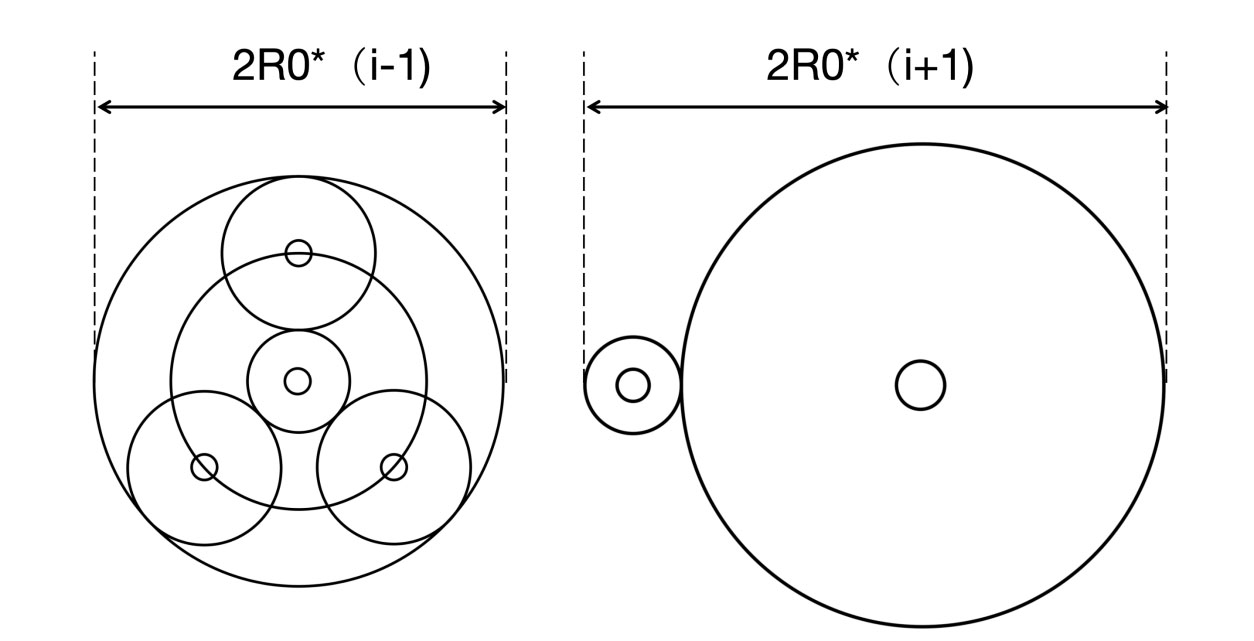
图7 相同减速比的单级行星减速机和平行轴减速机的尺寸对比